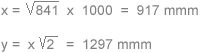VISTAS

Obtención de las vistas de un objeto

Generalidades

Se denominan vistas principales de un objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de cubo. También se podría definir las vistas como, las proyecciones ortogonales de un objeto, según las distintas direcciones desde donde se mire.

Las reglas a seguir para la representación de las vistas de un objeto, se recogen en la norma UNE 1-032-82, “Dibujos técnicos: Principios generales de representación”, equivalente a la norma ISO 128-82.

Denominación de las vistas

Si situamos un observador según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles de un objeto.

Estas vistas reciben las siguientes denominaciones:

Vista A: Vista de frente o alzado

Vista B: Vista superior o planta

Vista C: Vista derecha o lateral derecha

Vista D: Vista izquierda o lateral izquierda

Vista E: Vista inferior

Vista F: Vista posterior

Posiciones relativas de las vistas

Para la disposición de las diferentes vistas sobre el papel, se pueden utilizar dos variantes de proyección ortogonal de la misma importancia:

• El método de proyección del primer diedro, también denominado Europeo (antiguamente, método E)
• El método de proyección del tercer diedro, también denominado Americano (antiguamente, método A)

En ambos métodos, el objeto se supone dispuesto dentro de un cubo, sobre cuyas seis caras, se realizarán las correspondientes proyecciones ortogonales del mismo.

La diferencia estriba en que, mientras en el sistema Europeo, el objeto se encuentra entre el observador y el plano de proyección, en el sistema Americano, es el plano de proyección el que se encuentra entre el observador y el objeto.

El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas.

Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.

Una vez realizadas las seis proyecciones ortogonales sobre las caras del cubo, y manteniendo fija, la cara de la proyección del alzado (A), se procede a obtener el desarrollo del cubo, que como puede apreciarse en las figuras, es diferente según el sistema utilizado.

El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas.

Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.

Correspondencia entre las vistas

Como se puede observar en las figuras anteriores, existe una correspondencia obligada entre las diferentes vistas. Así estarán relacionadas:

1. El alzado, la planta, la vista inferior y la vista posterior, coincidiendo en anchuras.
2. El alzado, la vista lateral derecha, la vista lateral izquierda y la vista posterior, coincidiendo en alturas.
3. La planta, la vista lateral izquierda, la vista lateral derecha y la vista inferior, coincidiendo en profundidad.

Habitualmente con tan solo tres vistas, el alzado, la planta y una vista lateral, queda perfectamente definida una pieza. Teniendo en cuenta las correspondencias anteriores, implicarían que dadas dos cualquiera de las vistas, se podría obtener la tercera, como puede apreciarse en la figura:

También, de todo lo anterior, se deduce que las diferentes vistas no pueden situarse de forma arbitraria. Aunque las vistas aisladamente sean correctas, si no están correctamente situadas, no definirán la pieza.

TANGENTES

TANGENTES

RECTAS TANGENTES A CIRCUNFERENCIAS
DEFINICIONES: Una línea tangente es aquella línea que se encuentra a la misma distancia del centro que cualquier punto de la circunferencia.  Una línea que toque en un punto a una circunferencia o a un arco de circunferencia, es tangente a ellos y es perpendicular al radio que llega al punto de tangencia.

CONSTRUCCIONES

1. Dibujar una línea tangente a la circunferencia, que pase por el punto A.
PROCEDIMIENTO:
Dibujamos la circunferencia y localizamos el punto A, luego trazamos el radio OA. A este radio le levantamos una perpendicular en su extremo A, que será la tangente pedida.

2. Trazar una tangente a un arco de circunferencia cuyo centro no se conoce y que pase por el punto A.
PROCEDIMIENTO:
Situamos un punto B cualquiera sobre el arco. Con centro en este punto y radio AB trazamos un arco encontrando el punto C. Haciendo centro en A y radio AC trazamos un arco encontrando el punto D. Unimos los puntos A y D mediante una línea, hallando así la tangente.

3. Dado el segmento AB y una circunferencia O, trazar una tangente de tal manera que forme con AB un ángulo conocido.


PROCEDIMIENTO:
Trazamos la circunferencia y el segmento dado en el lugar indicado. Luego desde un punto cualquiera C, perteneciente a AB, trazamos un ángulo igual al dado, de tal forma que el otro lado del ángulo sea secante a la circunferencia, cortándola en los puntos D y E. Trazamos una perpendicular a la cuerda DE, que pase por el centro O de la circunferencia y la corte en el punto F. La tangente pedida (GH) será la que pase por F.

4.    Trazar una tangente a una circunferencia dada, que pase por un punto M fuera de ella.

PROCEDIMIENTO:
Trazamos una línea que una al punto M con el centro de la circunferencia.  Encontramos el punto medio A de la línea 0M y haciendo centro en este punto con el compás, y un radio igual a A0, trazamos un arco que cortará a la circunferencia en los puntos B y C.  Unimos el punto M con el punto B o con el punto C, encontrando así la tangente.

5. Dadas la circunferencia O y la línea AB, trazar una tangente a la circunferencia, que sea paralela a la línea AB.

PROCEDIMIENTO:
Trazamos una perpendicular a la línea AB, de tal forma que pase por el centro de la circunferencia y la corte en los puntos C y D. Trazando una perpendicular al radio que llega a cualesquiera de estos dos puntos, resultará la tangente pedida.
Nota: Observe en el procedimiento gráfico que es posible trazar dos tangentes a la circunferencia y que además sean paralelas a la línea AB: la que pasa por el punto D y la que pasa por el punto C.

 

6.   Trazar las tangentes exteriores a dos circunferencias dadas.

PROCEDIMIENTO:
Trazamos la línea 00’ que une los centros de las circunferencias y le hallamos su punto medio A.   Con centro en 0 y un radio igual a la  diferencia entre los radios de las circunferencias conocidas, trazamos una circunferencia auxiliar.   Con centro en A y radio A0, trazamos un arco que corte la circunferencia auxiliar en los puntos B y C. Trazamos y prolongamos las líneas radiales 0B y 0C para determinar sobre la circunferencia mayor los puntos D y E respectivamente.    A partir de 0’ trazamos los radios 0’F y 0’G paralelos a 0D y a 0E respectivamente.   Al unir D con F, y E con G resultarán las tangentes exteriores.
 

7. Trazar las tangentes interiores a dos circunferencias dadas.

PROCEDIMIENTO:
Trazamos la línea 00’ que une los centros de las circunferencias y le encontramos su punto medio A. Con centro en 0 y un radio igual a la  Suma de los radios de las circunferencias conocidas, trazamos una circunferencia auxiliar. Con centro en A y radio A0, trazamos un arco que corte la circunferencia auxiliar en los puntos B y C. Trazamos las líneas radiales 0B y 0C para determinar sobre la circunferencia O los puntos D y E respectivamente. A partir de 0’ trazamos los radios 0’F, paralelo a OE, y 0’G paralelo a 0D. Al unir D con G y E con F resultarán las tangentes interiores.

 

CIRCUNFERENCIAS TANGENTES A RECTAS

DEFINICIÓN: Cuando una circunferencia toca en un punto a una línea, y este punto está a igual distancia que los demás puntos de la circunferencia, entonces ésta es tangente a la línea.

CONSTRUCCIONES

1. Trazar una circunferencia tangente a los dos lados de un ángulo, que pase por el punto D que se encuentra sobre uno de los lados del ángulo.

 PROCEDIMIENTO:. Trazamos la bisectriz al ángulo dado y luego  levantamos  una  perpendicular al punto D, que corte a la bisectriz en el punto O.   Con centro en O y radio OD, trazamos la circunferencia tangente a los lados del ángulo. 

 

2. Trazar una circunferencia tangente a los lados de una línea poligonal cóncava de tres segmentos.

PROCEDIMIENTO:. Trazamos las bisectrices a cada uno de los ángulos formados por los segmentos, de tal forma que se corten en el punto O. A una de los segmentos, en este caso AB, le trazamos una perpendicular que pase por el punto O y corte al segmento en el punto E. Con centro en O y radio OE, trazamos la circunferencia tangente a los lados de la línea poligonal.
 

 

3. Trazar una circunferencia tangente a los tres lados de un triángulo.

 PROCEDIMIENTO:.
Trazamos las bisectrices a cada uno de los ángulos del triángulo ABC, las cuales se cortan en el punto O. A uno de los lados del triángulo, en este caso el AB, le trazamos una perpendicular que pase por el punto O y lo corte en el punto E.   Con centro en O y radio OE trazamos la circunferencia tangente.

 

4. Trazar tres circunferencias tangentes a los lados de un triángulo equilátero y tangentes entre sí. 

PROCEDIMIENTO:
Trazamos las líneas que unen cada vértice con el punto medio de su lado opuesto ( las medianas), las cuales se cortan en el punto O y a su vez cortan los lados del triángulo en los puntos 1,2 y 3. Trazamos una de las bisectrices de los ángulos que se forman en los cortes 1,2 y 3, en este caso en el corte 1. Esta bisectriz cortará a una de las medianas en el punto P, que será el centro de una de las circunferencias tangentes. Trasladamos este centro P a las demás medianas por medio de una circunferencia con centro en O, encontrando los otros centro P’ y P’’. Para encontrar el radio de las circunferencias tangentes, trazamos una perpendicular al lado AB del triángulo, que pase por el punto P y nos de el punto M. Las circunferencias tangentes se trazan con centro en los puntos P y con radio PM. 

 

CIRCUNFERENCIAS TANGENTES
DEFINICIÓN: Dos circunferencias son tangentes entre si cuando tienen solo un punto en común. La ubicación de los demás puntos de una con respecto a los demás de la otra, definen si son tangentes exteriores o interiores.

CONSTRUCCIONES

1. Dibujar dos circunferencias tangentes exteriores.

SOLUCION
Trazamos una línea OO’ con longitud igual a la suma de los radios de las circunferencias.   Con centro en los extremos de la línea y los radios respectivos, trazamos las circunferencias tangentes exteriores.

 

2. Trazar dos circunferencias tangentes interiores, de diferente radio.

PROCEDIMIENTO.

Trazamos la línea OO’ igual a la diferencia de los radios de las dos circunferencias.   Con centro en los extremos de la línea y los radios correspondientes trazamos las circunferencias tangentes interiores.

 

3. Dada una circunferencia trazarle circunferencias tangentes interiores, tangentes entre sí.

PROCEDIMIENTO
Dividimos la circunferencia en partes iguales, el doble del número de circunferencias pedidas.  En este caso dividimos la circunferencia en 6 partes, pues trazaremos 3 circunferencias tangentes. Dividida la circunferencia, trazamos los diámetros respectivos, prolongando uno de ellos hasta que forme el ángulo M con la tangente trazada al punto P de la circunferencia dada.   Trazamos la bisectriz del ángulo M, que corte al diámetro PQ en el punto F, centro de una de las circunferencias.   Los demás centros, F’ y F’’, los encontramos al cortar los otros diámetro con una circunferencia trazada desde O con radio OF.   Las circunferencias tangentes interiores las trazamos desde los puntos F,F’ y F’’, con radio FP.
 

4. Dibujar las circunferencias A,B y C tangentes exteriores.

PROCEDIMIENTO.

Trazamos el triángulo ABC, cuyos lados equivalen a las sumas de los radios de las circunferencias, a si:   lado AB igual a la suma de los radios de las circunferencias A y B, lado AC igual a la suma de los radios de las circunferencias A y C, y el lado BC igual a la suma de los radios de las circunferencias B y C.   Los vértices del triángulo serán los centros desde donde trazaremos las circunferencias con sus radios respectivos.

 

DIBUJO 2D , 3D Y 4D

Diferncia entre dibujo 2D, 3D y 4D

Una dimensión es cualquier extensión espacial medible, ya sea por su longitud, anchura, altura, profundidad, espesor…Los términos 2D, 3D y 4D se utilizan de acuerdo al número de dimensiones que retratan.

Si no entiendes la diferencia entre estos tres conceptos, a continuación te la aclaramos.

2D

Este término describe lo bidimensional, es decir; aquello que sólo tiene dos dimensiones. Aquello que se proyecta de manera plana en el espacio físico (así como los muñequitos de Las Chicas Superpoderosa.Por ejemplo, la fotografía o el dibujo de un auto suele ser bidimensional; porque por medio del dibujo solamente se puede ver y medir la longitud y la anchura; pero no se puede conocer su profundidad.

3D

Por otra parte, el término 3D se refiere a la tridimensionalidad. Es decir, a la forma en que percibimos nuestra realidad.

Se habla de que algo es tridimensional cuando tiene tres dimensiones, ya sea: longitud, anchura y profundidad.

tridimensional

Siguiendo con el ejemplo del auto, los coches que vemos pasar en nuestra realidad son tridimensionales; porque podemos medir cada una de las tres dimensiones antes mencionadas.

4D

A partir de lo que anteriormente hemos dicho, seguro que no es necesario aclarar a qué se refiere el término 4D; porque claramente describe la cuarta dimensión.

4d

La cuarta dimensión es un concepto abstracto, que deriva de la generalización de las reglas de la tridimensionalidad; añadiendo el factor del tiempo y del movimiento. Así por ejemplo, un objeto tridimensional que se mueve, se considera que tiene cuatro dimensiones.

El concepto 4D es muy difícil de entender, puesto que no es algo que puede ser captado en la realidad visible.

Diferencias clave entre 2D, 3D y 4D

• 2D = dos dimensiones, 3D = tres dimensiones y 4D = cuatro dimensiones.
• Los objetos bidimensionales (2D) se proyectan de forma plana y no se distingue su profundidad. Los objetos tridimensionales son aquellos de los cuales se conoce su anchura, profundidad y longitud. Los objetos tetradimensionales son aquellos a los que además de poderle medir los elementos que se le miden a los tridimensionales, también se les añade el factor del tiempo y el movimiento.
• 2D = plano, 3D = como la vida real y 4D = concepto abstracto.
• Ejemplos de figuras en 2D: cuadrado, triángulo, círculo.
• Ejemplos de figuras en 3D: cilindro, esfera, cubo, pirámide.
• Ejemplo de figura en 4D: 4 politopos de poliedros (compuestos por dos polígonos dimensionales).

Advertisement

FORMATOS

Formatos Normalizados Sistema ISO

Concepto

Se llama formato a la hoja de papel en que se realiza un dibujo, cuya forma y dimensiones en mm. están normalizados. En la norma UNE 1026-2 83 Parte 2, equivalente a la ISO 5457, se especifican las características de los formatos.

Dimensiones

Las dimensiones de los formatos responden a las reglas de doblado, semejanza y referencia. Según las cuales:

1. Un formato se obtiene por doblado transversal del inmediato superior.
2. La relación entre los lados de un formato es igual a la relación existente entre el lado de un cuadrado y su diagonal, es decir 1/√2 .
3. Y finalmente para la obtención de los formatos se parte de un formato base de 1 m².

Aplicando estas tres reglas, se determina las dimensiones del formato base llamado A0 cuyas dimensiones serían 1189 x 841 mm.

El resto de formatos de la serie A, se obtendrán por doblados sucesivos del formato A0.

La norma estable para sobres, carpetas, archivadores, etc. dos series auxiliares B y C.

Las dimensiones de los formatos de la serie B, se obtienen como media geométrica de los lados homólogos de dos formatos sucesivos de la serie A.

Los de la serie C, se obtienen como media geométricas de los lados homólogos de los correspondientes de la serie A y B.

Excepcionalmente y para piezas alargadas, la norma contempla la utilización de formatos que denomina especiales y excepcionales, que se obtienen multiplicando por 2, 3, 4 … y hasta 9 veces las dimensiones del lado corto de un formato.

Plegado

La norma UNE – 1027 – 95, establece la forma de plegar los planos. Este se hará en zig-zag, tanto en sentido vertical como horizontal, hasta dejarlo reducido a las dimensiones de archivado. También se indica en esta norma que el cuadro de rotulación, siempre debe quedar en la parte anterior y a la vista.

Indicaciones en los formatos

Márgenes

En los formatos se debe dibujar un recuadro interior, que delimite la zona útil de dibujo. Este recuadro deja unos márgenes en el formato, que la norma establece que no sea inferior a 20 mm. para los formatos A0 y A1, y no inferior a 10 mm. para los formatos A2, A3 y A4. Si se prevé un plegado para archivado con perforaciones en el papel, se debe definir un margen de archivado de una anchura mínima de 20 mm., en el lado opuesto al cuadro de rotulación.

Cuadro de rotulación

Conocido también como cajetín, se debe colocar dentro de la zona de dibujo, y en la parte inferior derecha, siendo su dirección de lectura, las misma que el dibujo. En UNE – 1035 – 95, se establece la disposición que puede adoptar el cuadro con su dos zonas: la de identificación, de anchura máxima 170 mm. y la de información suplementaria, que se debe colocar encima o a la izquierda de aquella.

Señales de centrado

Señales de centrado. Son unos trazos colocados en los extremos de los ejes de simetría del formato, en los dos sentidos. De un grosor mínimo de 0,5 mm. y sobrepasando el recuadro en 5 mm. Debe observarse una tolerancia en la posición de 0,5 mm. Estas marcas sirven para facilitar la reproducción y microfilmado.

Señales de orientación

Señales de orientación. Son dos flechas o triángulos equiláteros dibujados sobre las señales de centrado, para indicar la posición de la hoja sobre el tablero.

Graduación métrica de referencia

Graduación métrica de referencia. Es una reglilla de 100 mm de longitud, dividida en centímetros, que permitirá comprobar la reducción del origina en casos de reproducción.

LETRA NORMALIZADA

LETRA TÉCNICA

CALIGRAFÍA

TÉCNICA

La letra técnica es parte integral de un dibujo ya que explica algunos aspectos, señala dimensiones y forma parte de una presentación. Por eso una letra técnica mal realizada, rebaja la calidad del trabajo en general.

La utilidad de la letra técnica indicar por escrito toda la información necesaria de un Dibujo y el nombre es porque el tipo de letras y números deben trazarse de acuerdo con las técnicas.

ESTILOS DE LETRAS

ASPECTOS IMPORTANTES EN LA LETRA TÉCNICA.

1. Conocer sus formas y proporciones correcta.

2. Orden y sentido de los trazos.

3. Uniformidad (altura, inclinación, intensidad y peso de las líneas, espaciamiento entre letras y palabras, apariencia.)

4. La práctica persistente.

HISTORIA DE LA LETRA TÉCNICA.

Siglo XIX, desarrollo industrial y del Dibujo Técnico.

Necesidad de una letra sencilla, legible.

Alfabeto de letras mayúsculas y minúsculas inclinadas y rectas.

Estilo gótico con trazos sistemáticos.

ESTANDARIZACIÓN DE LAS LETRAS (DIN) (ASA)

American Standards Association (ASA, 1935) Estandariza.

Comité de normas Alemanas (DIN, 1916)

ESCRITURA NORMALIZADA DIN 16 Y DIN 17

Las normas para la DIN 16 y DIN 17 fueron revisadas y reformadas por la DIN en 1968 y se creó la norma DIN 6775, serie 1, que concuerda con la ISO del número 398/1. La razón fundamental fue el microfilmado.

La antigua DIN 16 y DIN 17 y la nueva norma 6775 se diferencian en cuanto al valor de la medida nominal h. En aquellas, las relación de la altura nominal era de 7/7; en la nueva, la relación de la altura nominal es de 10/10.

No se permite utilizar ambos estilos en un mismo dibujo y el subrayarlas.

TECNICA DE LETRA TECNICA A MANO ALZADA

La técnica a mano alzada permite al delineante el trazo de líneas verticales, horizontales e inclinadas solo con el equipo de trazar y el papel. Esta técnica es el principal antecedente para la realización de los ejercicios de la letra normalizada que se utiliza.

Para el trazo a mano libre, el lápiz o rapidografo debe de tomarse con libertad, para ello no debe tomarse cerca de la punta, sino un poco más arriba (3 cm. Aprox.). La distancia entre los ojos y la pluma debe ser de unos 30 cm. La luz debe entrar por la izquierda (derecha). Se rotula mejor sentado que dé pie. El cuerpo de frete a la escritura. Respiración lenta y rítmica. Descansos después de 30 minutos.

El lápiz debe tener punta cónica de dureza 2B o HB. Limpiarlo periódicamente

LETRA TECNICA A LÁPIZ.

Cuando se trabaja a lápiz se deben procurar trazos oscuros y nítidos, un trazo suave producirá letras grises e imprecisas. El orden de los trazos y las dimensiones de las letras deben aprenderse practicando inicialmente con el lápiz antes de ensayar con tinta.

La mina debe afilarse de forma que se obtenga una larga punta cónica. La presión del lápiz sobre el papel debe ser lo más uniforme posible y es conveniente acostumbrarse a hacer rodar el lápiz entre los dedos cada tres o cuatro trazos, para conseguir una mayor uniformidad. El lápiz debe sostenerse en la mano con la fuerza mínima necesaria para controlar los trazos.

Instrumentos de Dibujo

HERRAMIENTAS E INSTRUMENTOS PARA DIBUJO TECNICO

Estándar

1. Tablero de dibujo
Es un instrumento de dibujo sobre el que se fija el papel para realizar el dibujo, permite el desplazamiento de la regla T, debe ser construido de modo tal que no se produzcan dobladuras ni pandeos; debe ser inclinada

.
.

2. La regla t
La regla T recibe ese nombre por su semejanza con la letra T. Posee dos brazos perpendiculares entre sí. El brazo transversal es más corto. Se fabrican de madera o plástico. Se emplea para trazar líneas paralelas horizontales en forma rápida y precisa.
También sirve como punto de apoyo a las escuadras y para alinear el formato y proceder a su fijación.

3. Regla graduada
Es un instrumento para medir y trazar líneas rectas, su forma es rectangular, plana y tiene en sus bordes grabaciones de decímetros, centímetros y milímetros..
Sus longitudes varían de acuerdo al uso y oscilan de 10 a 60 centímetros Las más usuales son las de 30 centímetros.

4. Las escuadras
Las escuadras se emplean para medir y trazar líneas horizontales, verticales, inclinadas, y combinada con la regla T se trazan líneas paralelas, perpendiculares y oblicuas.
Las escuadras que se usan en dibujo técnico son dos:
– La de 45º que tiene forma de triángulo isósceles con ángulo de 90º y los otros dos de 45º.
– La escuadra de 60º llamada también cartabón que tiene forma de triángulo escaleno, cuyos ángulos miden 90º, 30º y 60º.

5. El transportador
Es un instrumento utilizado para medir o transportar ángulos. Son hechos de plástico y hay de dos tipos: en forma de semicírculo dividido en 180º y en forma de círculo completo de 360º

.

6. Escalímetro
Los escalímetros son instrumentos de medición, semejantes a una regla, más utilizado es el de forma triangular; tiene, generalmente, una longitud de 30 cms., consta de tres caras y en cada cara posee dos escalas.

7. El compás
Es un instrumento de precisión que se emplea para trazar arcos, circunferencias y transportar medidas.

Clases de compás.

• Compás de pieza: es el compás normal que al que se le puede colocar los accesorios como el portaminas o lápiz.

• Compás de puntas secas: posee en ambos extremos puntas agudas de acero y sirve para tomar o trasladar medidas.

• Compás de bigotera: se caracteriza por mantener fijos los radios de abertura. La abertura de este compás se gradúa mediante un tornillo o eje roscado. Es utilizado para trazar circunferencias de pequeñas dimensiones y circunferencias de igual radio.

• Compás de bomba: se utiliza para trazar arcos o circunferencias muy pequeñas. Está formado por un brazo que sirve de eje vertical para que el portalápiz gire alrededor de él.

8. Lápices
Los lápices son elementos esenciales para la escritura y el dibujo. Están formados por una mina de grafito y una envoltura de madera.

9. Grados de dureza de la mina
La mina de los lápices posee varios grados desde el más duro hasta el más blando. Con los de mina dura se trazan líneas finas de color gris y las más blandas líneas gruesas y de color negro.
Están clasificados por letras y números. La H viene de la palabra hard que significa duro, la F significa firme y la B de black que significa negro.
Los más duros son: 4H, 3H, 2H y H. Los intermedios son: HB y F. Los más blandos son: B, 2B, 3B y 4B.

10. Portaminas o lapiceros
Los portaminas son de metal o plástico y aloja en su interior la mina o minas que se deslizan mediante un resorte hacia afuera, que han de servir para escribir o trazar.

11. Goma de borrar
Las gomas de borrar se emplean para hacer desaparecer trazos incorrectos, errores, manchas o trazos sobrantes. Por lo general son blandas, flexibles y de tonos claros para evitar manchas en el papel.

.

12. El papel
El papel es una lámina fina hecha de unas pastas de materiales distintos como trapos, madera, cáñamo, algodón y celulosa de vegetales. Es utilizado en todo el mundo para escribir, imprimir, pintar, dibujar y otros.

13. El tirro o cinta adhesiva
El papel se fijará al tablero gracias a la cinta adhesiva o tirro, la cual, si es de buena calidad no dejará huella ni en el papel ni en el tablero.

14. Curvígrafos
Plantilla que sirve para trazar curvas, estando estas definidas sobre sus bordes o bien formando huecos.

15. Plumas para tinta china
Los instrumentos modernos, que están a disposición de los dibujantes profesionales, ayudan en la precisión, perfección y limpieza del trabajo.

16. Tinta para dibujo
La tinta para dibujo es un polvo de carbón finamente dividido, en suspensión, con un agregado de goma natural o sintética para impedir que la mezcla se corra fácilmente con el agua.

17. Plantillas
Se usan para dibujar formas estándares cuadrados, hexagonales, triangulares y elípticos. Estas se usan para ahorrar tiempo y para mayor exactitud en el dibujo.

18. Sacapuntas
Después de haber cortado la madera de un lápiz con una navaja o sacapuntas mecánico, se debe afinar la barra de grafito del lápiz y darle una larga punta cónica.

Dibujo asistido por computador
A través de programa AUTOCAD